How Long From Cold to Warm

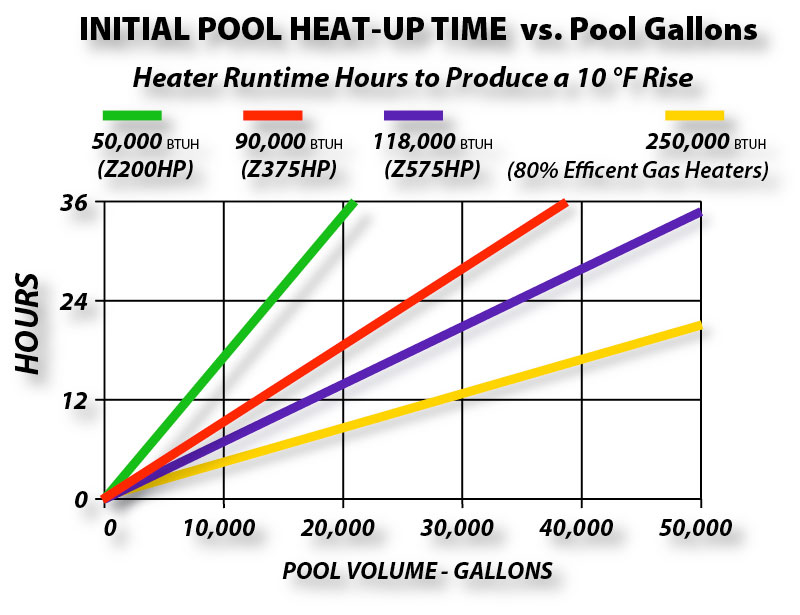
The graph above shows how many hours it would take each of 4 pool heaters with various heat outputs to raise the temperature of a given pool volume (gallons) by 10°F.

When you first open your pool or when it has lost all of its heat, the water will typically be about the same as the average daily air temperature for UNCOVERED pools and about 10 °F warmer for COVERED pools.

If you assume that a cover is in place for the initial heat-up then heat losses can be basically eliminated from consideration with very little error. Even with no cover there is a relatively small added heat loss to make up as the water gets warmer, so the times shown by this graph are fairly close and still useful.

CONCLUSIONS: Even a big gas heater takes a long time to heat up all but the smallest pools. A properly sized HEAT SIPHON should take no more than 2 to 3 days to initially heat up your pool. MOST IMPORTANT THOUGH IS THE FACT THAT HEAT SIPHON MAKES 24/7 - 85°F AFFORDABLE!!

HEAT SIPHON FAST FACTS - A 5HP HEAT SIPHON will take about 18 hours to heat-up a 25,000 gallon pool by 10°F (typical 18ft x 36 ft with an average depth of around 5 feet). That's 2.1 MILLION BTU's , BUT once heated to 82°F and covered with a solar blanket 12 hours a day, it only takes 25% of that amount of heat per DAY to MAINTAIN 82°F in 72 °F air. Runtime 4.5 Hours/day COST= $2.86/day @$.10/kwh)

What Pool Temperature is Most Commonly Preferred?

We are asked this question quite a lot by first time pool owners, and here is what we have found after 30 years of sizing Heat Siphon's and talking to our customers:

As it turns out most pool owners want their pools about 10-15°F warmer than the average daytime air temperature.

In the northeastern US where the air at swim temp is about 70°F, the most preferred swimming temperature is 80°F.

As you move south the average air temperature increases as does the preferred pool temperature. For example in Miami, Fl many pool owners prefer their pools in the high 80's to low 90's.

Although it appears to be a crude method at first, the simple old gas heater sizing method of "WHAT DEGREE RISE DO YOU WANT?" requiring a heater to provide enough heat to maintain a certain degree rise seems to make some sense.

But we use the computer modeled state of the art Heat Siphonalysis (HSA) which calculates the radiation, convection and conduction heat loss from your pool using YOUR surface area, local air temperature and humidity based on YOUR climate data and YOUR utility costs to get a VERY ACCURATE heat loss and sizing.

Thats why we GUARANTEE our sizing program will pick the correct model OR YOU CAN RETURN IT

What SIZE HEAT SIPHON Do You Need? - Get a FREE HSA

We will email or FAX you the results for your pool. Click here.